String #
This page contains the following content:
Equals #
This measure compares two strings using exact matching. The comparison can be case-sensitive or insensitive. The resulting similarity can only be \(1\) or \(0\) .
The following parameters can be set for this similarity measure.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| caseSensitive | Flag (boolean) | true | The parameter is used to define, whether a comparison is case-sensitive or insensitive. |
In sim.xml this measure can be defined as follows:
<StringEqual name="SMStringEquals" class="String" caseSensitive="true"/>
At runtime, the measure can be defined as follows:
SMStringEqual smStringEquals = (SMStringEqual) SimilarityModelFactory.getDefaultSimilarityModel().createSimilarityMeasure(
SMStringEqual.NAME,
ModelFactory.getDefaultModel().getStringSystemClass()
);
smStringEquals.setCaseSensitive();
simVal.getSimilarityModel().addSimilarityMeasure(smStringEquals, "SMStringEquals");
N-Gram #
This measure computes the n-gram similarity of two strings. It splits both strings into all possible substrings of length n and computes a distance based on the number of identical sub-strings. The distance is normalized by division through the number of the maximum n-grams of both substrings. The comparison can be case-sensitive or insensitive. The similarity is computed as follows:
\(sim(q,c) = \frac{\bigl|nGrams_{q} \ \cap \ nGrams_{c}\bigl|}{\bigl|nGrams_{q} \ \cup \ nGrams_{c}\bigl|}\)So, the similarity will be \(1\) , if a matching partner for each n-gram exists, or \(0\) , if any mapping partner for any n-gram was found. If the value for n is higher than the length of the strings, an invalid similarity will be returned.
The following parameters can be set for this similarity measure.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| caseSensitive | Flag (boolean) | true | The parameter is used to define, whether a comparison is case-sensitive or insensitive. |
| n | Size (int) | 1 | The parameter expects an Integer value given, that defines the size of the n-grams used for the similarity computation. |
In sim.xml this measure can be defined as follows:
<StringNGram name="SMStringNGram" class="String" caseSensitive="false" n="3" default="false"/>
At runtime, the measure can be defined as follows:
SMStringNGram smStringNGram = (SMStringNGram) simVal.getSimilarityModel().createSimilarityMeasure(
SMStringNGram.NAME,
ModelFactory.getDefaultModel().getStringSystemClass()
);
smStringNGram.setCaseInsensitive();
smStringNGram.setN(3);
simVal.getSimilarityModel().addSimilarityMeasure(smStringNGram, "SMStringNGram");
For example, two strings q=“Cake” and c=“ProCAKE” are compared. Using the shown measure definition, n is set to \(3\) , so n-grams of this size will be created. For q, these are “Cak” and “ake”, and for c, “Pro”, “roC”, “oCA”, “CAK”, “AKE”. Because the case is insensitive, two matching pairs “Cak” and “ake” can be found. So, the similarity will be computed as follows: \(\frac{2}{5} = 0.4\) .
Levenshtein #
This measure compares two strings using the Levenshtein algorithm. The comparison can be case-sensitive or insensitive. The Levenshtein distance \(LD\) computes the distance between a source string (s) and a target string (t). The distance is the number of deletions, insertions, or substitutions required to transform s into t. The similarity between s and t is defined as \(sim(s,t) = 1-\frac{LD(s,t)}{max(length(s),length(t))}\) .
It is also possible to define a threshold for this measure. This is a maximum bound for the distance. If the distance is higher than the threshold value, the similarity will be \(0.0\) .
The following parameters can be set for this similarity measure.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| caseSensitive | Flag (boolean) | true | The parameter is used to define, whether a comparison is case-sensitive or insensitive. |
| threshold | Size (int) | -1 | The parameter expects an Integer value given, that defines the maximum bound for the distance. If the distance is higher than the threshold value, the similarity will be \(0.0\) . |
In the sim.xml this measure is defined as follows:
<StringLevenshtein name="SMStringLevenshtein" class="String" threshold="10" caseSensitive="false"/>
At runtime, the measure can be defined as follows:
SMStringLevenshtein smStringLevenshtein = (SMStringLevenshtein) simVal.getSimilarityModel().createSimilarityMeasure(
SMStringLevenshtein.NAME,
ModelFactory.getDefaultModel().getStringSystemClass()
);
smStringLevenshtein.setCaseInsensitive();
smStringLevenshtein.setThreshold(10);
simVal.getSimilarityModel().addSimilarityMeasure(smStringLevenshtein, "SMStringLevenshtein");
For example, if two strings s=“CAKE” and t=“case” are compared, their similarity is \(sim(s,t) = 1-\frac{1}{4}=0.75\) , as only one character needs to be substituted.
Jaro Winkler #
This measures compares two strings using the Jaro Winkler distance. The comparison can be case-sensitive or insensitive.
This measure is based on the Jaro similarity, which is the weighted sum of percentage of the number of matched characters \(m\) and half the number of transposed characters \(t\) between two given strings \(s_{1}\) and \(s_{2}\) . The similarity is defined as:
\(sim_{j}(s_{1},s_{2}) = \begin{cases} 0 &\text{, if } m = 0 \\ \frac{ 1 }{ 3 } * ( \frac{ m }{ |s_{1}| } + \frac{ m }{ |s_{2}| } + \frac{ m-t }{ m } ) &\text{, otherwise } \end{cases}\)Here, \(|s_{i}|\) is the length of the string \(s_{i}\) .
For example, comparing the two strings “CAKE” and “CASE”. Here, \(m\) is 3 and \(|s_{1}| = |s_{2}| = 4\) . \(t\) is \(\frac{1}{2}\) , which is smaller than 1. So, \(t\) is \(0\) . Therefore, the Jaro similarity is \(\frac{ 1 }{ 3 } * ( \frac{ 3 }{ 4 } + \frac{ 3 }{ 4 } + \frac{ 4-0 }{ 4 } ) = \frac{5}{6} \approx 0.8333 \) .
This measure was extended by Winkler to the Jaro Winkler similarity by the matching of initial characters. This uses a prefix scale \(p\) , which gives more favorable ratings to strings that match from the beginning for a given prefix length \(l\) . The similarity is defined as:
\(sim_{jw}(s_{1},s_{2}) = sim_{j}(s_{1},s_{2}) + l * p * (1 * sim_{j}(s_{1},s_{2}))\)The standard value for \(p\) is \(0.1\) , which is also used in this implementation. \(l\) is limited to a maximum value of 4 characters.
Continuing the example, \(l\) is 2, because the first two characters does match and the third does not. So, the Jaro Winkler similarity is \(sim_{jw}(s_{1},s_{2}) = \frac{5}{6} + 2 * 0.1 * (1 - \frac{5}{6}) = \frac{13}{15} \approx 0.8667\) .
The following parameters can be set for this similarity measure.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| caseSensitive | Flag (boolean) | true | The parameter is used to define, whether a comparison is case-sensitive or insensitive. |
A Jaro Winkler measure with a case-sensitive can be created in the sim.xml as follows:
<StringJaroWinkler name="SMStringJaroWinkler" class="String" caseSensitive="true" default="false"/>
At runtime, the measure can be defined as follows:
SMStringJaroWinkler smStringJaroWinkler = (SMStringJaroWinkler) simVal.getSimilarityModel().createSimilarityMeasure(
SMStringJaroWinkler.NAME,
ModelFactory.getDefaultModel().getStringSystemClass()
);
simVal.getSimilarityModel().addSimilarityMeasure(smStringJaroWinkler, "SMStringJaroWinkler");
Term Count #
This measure compares two strings by simply counting the number of terms. One term is identified by the specified delimiter. The similarity between query and case is defined as the distance between term counts: \(sim(q,c) = 1 - \frac{abs(length(q) - length(c)}{max(length(q), length(c))}\) .
The following parameters can be set for this similarity measure.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| delimiter | Delimiter (String) | | The parameter expects a String, which is used, to identify the several terms in query and case. |
In the sim.xml this measure is defined as follows:
<StringTermCount name="SMStringTermCount" class="String" delimiter=" "/>
At runtime, the measure can be defined as follows:
SMStringTermCount smStringTermCount = (SMStringTermCount) simVal.getSimilarityModel().createSimilarityMeasure(
SMStringTermCount.NAME,
ModelFactory.getDefaultModel().getStringSystemClass()
);
smStringTermCount.setDelimiter(" ");
simVal.getSimilarityModel().addSimilarityMeasure(smStringTermCount, "SMStringTermCount");
Consider two different strings \(query=\) "ProCAKE", \(case1=\) "Test", the similarity \(sim(query,case1)=1\) , as both strings contain only one term. If a different string \(case2=\) "ProCAKE is a CBR framework" is compared to the query, \(sim(query,case2)=1 - \frac{abs(1 - 5)}{max(1, 5)}=1-\frac{4}{5}=0.2\) , as both strings differ substantially, when only taking their number of terms into account with a blank as delimiter.
Cosine #
This measure compares a query to a case through a bag of words approach. In this measure the similarity is calculated by a cosine measure:
\(sim(q,c) = \frac{\sum_{i=1}^{n}q_{i} * c_{i}}{\sqrt{\sum_{i=1}^{n}(q_{i})^{2}} * \sqrt{\sum_{i=1}^{n}(c_{i})^{2}}}\) .
To calculate the similarity, the case and query strings are separated into tokens by a user-defined regex delimiter.
It is also possible to define the case sensitivity and insensitivity of the measure to determine the token comparison. Then the term frequency is defined for each token from each string to calculate the cosine similarity
The following parameters can be set for this similarity measure.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| caseSensitive | Flag (boolean) | false | The parameter is used to define, whether a comparison is case-sensitive or insensitive. |
| delimiter | Delimiter (String) | | The parameter expects a String, which is used, to identify the several terms in query and case. |
In the sim.xml this measure can be defined with a whitespace as delimiter and case-sensitive as follows:
<StringCosine name="SMStringCosine" class="String" delimiter=" " caseSensitive="true"/>
At runtime, the measure can be defined as follows:
SMStringCosine smStringCosine = (SMStringCosine) simVal.getSimilarityModel().createSimilarityMeasure(
SMStringCosine.NAME,
ModelFactory.getDefaultModel().getStringSystemClass()
);
smStringCosine.setForceOverride(true);
smStringCosine.setDelimiter(" ");
smStringCosine.setCaseSensitive();
simVal.getSimilarityModel().addSimilarityMeasure(smStringCosine, "SMStringCosine");
As example for the defined measure StringCosine, with a given query=“Knowledge Engine” and case=“Knowledge engine” the similarity would be 0.5. In this case the bag of words contains three tokens, because the measure is case-sensitive: Knowledge, Engine, engine. Query and case have one token in common and both frequency-vectors have a length of two, so the cosine measure would calculate:
\(sim(q,c) = \frac{1}{ \sqrt{2} * \sqrt{2} }\) .
If the case had been “Knowledge Engine”, the similarity would have been 1.0, because they have two Tokens out of two in common:
\(sim(q,c) = \frac{2}{ \sqrt{2} * \sqrt{2} }\) .
Isolated Mapping #
This measure tokenizes a query and case string based on a given regex delimiter and calculates the similarity between the collection of tokens analogous to CollectionIsolatedMapping.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| delimiter | Delimiter (String) | \s+ | The parameter expects a regular expression as String, which is used to tokenize the query and case string. |
| similarityToUse | Similarity Measure (String) | null | The parameter is used to define, which similarity measure is used for the similarity computation between the tokens. The similarity measure, which is referred, must exist in the runtime domain, too. Otherwise, an exception will be thrown. If no similarityToUse is defined, an exception will be thrown. |
In the sim.xml this measure can be defined with the default whitespace regex as delimiter and StringLevenshtein for token similarity as follows:
<StringLevenshtein name="MyStringLevenshteinSim" class="String" default="false" threshold="1" caseSensitive="false"/>
<StringIsolatedMapping name="MyStringIsolatedMappingSim" class="String" delimiter="\s+" similarityToUse="SMStringLevenshtein" />
At runtime, the analogous measure can be defined as follows:
SMStringLevenshtein smLevenshtein = (SMStringLevenshtein) SimilarityModelFactory.getDefaultSimilarityModel()
.createAndRegisterSimilarityMeasure(
"MyStringLevenshteinSim",
SMStringLevenshtein.NAME,
ModelFactory.getDefaultModel().getStringSystemClass()
);
smLevenshtein.setThreshold(1);
smLevenshtein.setCaseInsensitive();
SMStringIsolatedMapping smStringIsolatedMapping = (SMStringIsolatedMapping) SimilarityModelFactory.getDefaultSimilarityModel()
.createAndRegisterSimilarityMeasure(
"MyStringIsolatedMappingSim",
SMStringIsolatedMapping.NAME,
ModelFactory.getDefaultModel().getStringSystemClass()
);
smStringIsolatedMapping.setSimilarityToUse("MyStringLevenshteinSim");
smStringIsolatedMapping.setDelimiter("\\s+");
Regular Expressions #
This measure compares a case to a query, which is written as a regular expression. A regular expression is a sequence of characters that define a pattern. There are three implemented kinds of syntax:
- EGREP
- PERL 5
- POSIX
The default syntax is PERL5. The different types of syntax support several expressions. These are listed in the Java documentation. The regular expression query can only indicate whether an expression matches or not. So the similarity can only be \(1\) or \(0\) .
The following parameters can be set for this similarity measure.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| syntax | Syntax (String) | perl5 | The parameter is used to define, which syntax is used for the regular expression. Three kinds of syntax are available: egrep, perl5 and posix. |
In the sim.xml this measure is defined as follows:
<StringRegexp name="SMStringRegexp" class="String" syntax="egrep"/>
At runtime, the measure can be defined as follows:
SMStringRegexp smStringRegexp = (SMStringRegexp) simVal.getSimilarityModel().createSimilarityMeasure(
SMStringRegexp.NAME,
ModelFactory.getDefaultModel().getStringSystemClass()
);
smStringRegexp.setSyntax(RegExpSyntax.EGREP);
simVal.getSimilarityModel().addSimilarityMeasure(smStringRegexp, "SMStringRegexp");
For example, “.” is a regular expression, which works with all 3 kinds of syntax. It matches any single character at this position. If there is a string s=“C.KE” in the query, it would match with a case s=“CAKE”, so the similarity would be 1.0.
Wildcard #
This measure compares a query and case string, where the query can contain wildcards. Wildcards are a kind of regular expression. Therefore, they are implemented by using the regular expression syntax PERL5. So, the Wildcard measure is a limited kind of the Regular Expressions measure.
There are only two supported kinds of wildcards:
*matches zero, one or more arbitrary symbols.?matches exactly one arbitrary symbol.
The wildcard query can only indicate, if an expression matches or not. So the similarity can only be \(1\)
or \(0\)
. In the sim.xml this measure is defined as follows:
<StringWildcard name="SMStringWildcard" class="String"/>
At runtime, the measure can be defined as follows:
SMStringWildcard smStringWildcard = (SMStringWildcard) simVal.getSimilarityModel().createSimilarityMeasure(
SMStringWildcard.NAME,
ModelFactory.getDefaultModel().getStringSystemClass()
);
simVal.getSimilarityModel().addSimilarityMeasure(smStringWildcard, "SMStringWildcard");
For example, a string s=“C?KE” would match a string s=“CAKE”, so the similarity is 1.0. A string s="*" would match with any possible string, the similarity would always be 1.0.
Table #
For unordered symbolic types with a known set of attribute values a tabular similarity measure can be defined. However, this approach is only feasible if the symbol type only contains a few values, since the knowledge acquisition effort increases quadratically.
For the set of attribute values \({T_A}_i = {v_1,... , v_k}\)
a \(k \times k\)
matrix \(S = [s_{ij}]\)
with \(0 \leq s_{ij} \leq 1\)
defines the similarity values as \({sim_A}_i(x,y) = s_{xy}\)
. If no corresponding entry is set, the similarity of an object to itself is always 1.0.
The following parameters can be set for this similarity measure.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| symmetric | Flag (boolean) | true | The parameter is used to define, whether similarity computations should be symmetric or not. If the value is set to false, an extra similarity value needs to be defined for each direction of comparison. |
In the sim.xml this measure is defined as follows:
<TableDataObject name="SMTableDataObject" class="CarType" symmetric="false">
<Entry query="sports car" case="sports car" value="1.0"/>
<Entry query="town car" case="town car" value="1.0"/>
<Entry query="mini van" case="mini van" value="1.0"/>
<Entry query="sports car" case="town car" value="0.5"/>
<Entry query="sports car" case="mini van" value="0.1"/>
<Entry query="town car" case="mini van" value="0.8"/>
</TableDataObject>
This example measure requires a String class called CarType, which has to be defined in the model.xml. In this case, this can look like:
<StringClass name="CarType">
<InstanceEnumerationPredicate>
<Value v="sports car"/>
<Value v="town car"/>
<Value v="mini van"/>
</InstanceEnumerationPredicate>
</StringClass>
If there is a similarity calculation, where query and case have no entry, the similarity is always 0.0. So, the similarity for a query, which contains a TownCar object, and a case, which contains a SportsCar object, is 0.0. If query and case are objects with the same value and no similarity is defined, the default similarity for this case is 1.0.
At runtime, the measure can be defined as follows:
SMTableDataObject smTableDataObject = (SMTableDataObject) simVal.getSimilarityModel().createSimilarityMeasure(
SMTableDataObject.NAME,
ModelFactory.getDefaultModel().getClass("CarType")
);
smTableDataObject.setSymmetric(false);
smTableDataObject.addSimilarity(townCar, townCar, 1.0);
smTableDataObject.addSimilarity(sportsCar, townCar, 0.5);
smTableDataObject.addSimilarity(sportsCar, miniVan, 0.1);
smTableDataObject.addSimilarity(townCar, miniVan, 0.8);
simVal.getSimilarityModel().addSimilarityMeasure(smTableDataObject, "SMTableDataObject");
Here, townCar, sportsCar and miniVan need to be atomic objects of the class CarType. Otherwise, this would cause an exception.
Taxonomy #
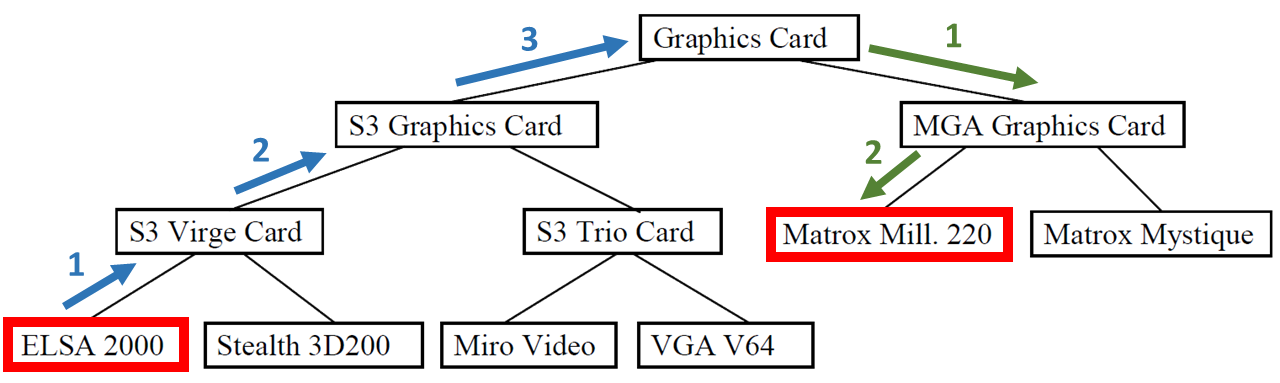
To use any of these measures, it is necessary to create a taxonomy order in the model.xml. This is explained on this page. The following examples require a string class called GraphicsCard, which can look like:
<StringClass name="GraphicsCard">
<InstanceTaxonomyOrderPredicate>
<Node v="Graphics Card">
<Node v="S3 Graphics Card">
<Node v="S3 Virge Card">
<Node v="ELSA 2000"/>
<Node v="Stealth 3D200"/>
</Node>
<Node v="S3 Trio Card">
<Node v="Miro Video"/>
<Node v="VGA V64"/>
</Node>
</Node>
<Node v="MGA Graphics Card">
<Node v="Matrox Mill. 220"/>
<Node v="Matrox Mystique"/>
</Node>
</Node>
</InstanceTaxonomyOrderPredicate>
</StringClass>
The class TaxonomyUpdater can also be used to create taxonomies. In it, a taxonomy can be created that contains both, the node values and the node similarity weights. From this, the model and the sim model can be created. The application of the TaxonomyUpdater is described here.
The following parameters exist for all taxonomy implementations.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| class | Class (String) | null | The parameter is used to define, for which data class the similarity measure will be applied. Here, the classes must have a taxonomic order. |
Classic #
The classic taxonomy measure is calculated by pre-initialized node weights. All nodes of one level have the same weight, which can be calculated by the following function:
\(weight(node) = \frac{height(node)}{maxlevels - 1} - \frac{1}{maxlevels - 1}\)The value maxlevels denotes the number of levels in the taxonomy and the function height starts with 1 for the root and increases the height for each level, e.g., the children of root have a height of 2.
Additional strategies enable customizing the similarity measure. If query and case are arranged hierarchically one below the other in the taxonomy, different strategies can be applied either to case or query. Three different parameters can be chosen for specifying which weight node has to be taken:
Optimistic: the similarity is always \(1.0\) .
Pessimistic: the lowest weight of the common father node or the lower node is taken.
Average: the average of the whole node path is calculated and taken as similarity value.
Below is an example of a taxonomy. It was also used to create the test classes.
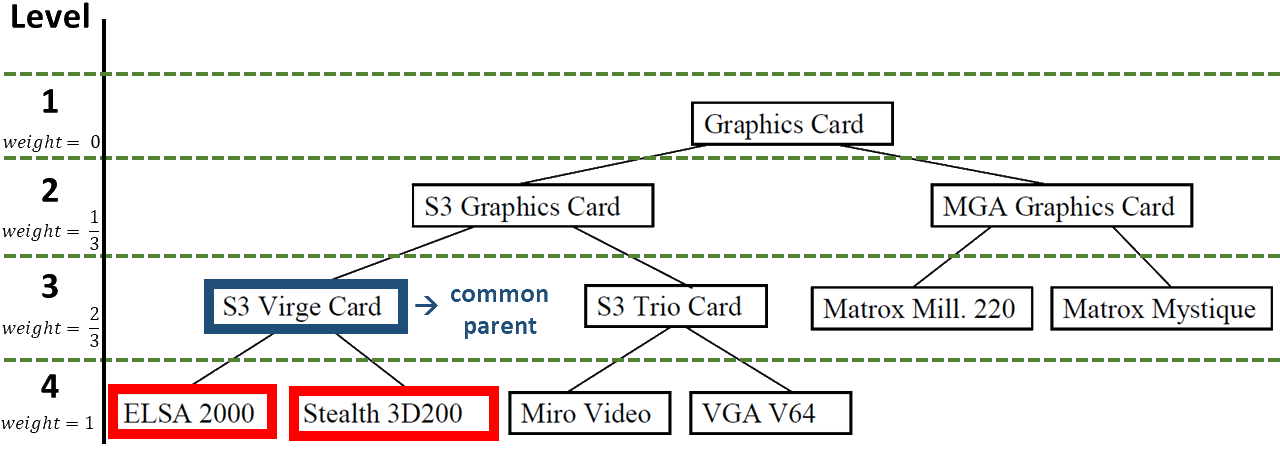
To calculate the similarity between the nodes ELSA 2000 and Stealth 3D200, the weight of the common parent, S3 Virge Card, is used. There are 4 levels in this taxonomy, the parent node is at level 3. So its weight is calculated as follows: \(\frac{3}{4 - 1} - \frac{1}{4 - 1}\) . The result is \(\frac{2}{3}\) .
When calculating the similarity between an inner node and one of its ancestors, the different strategies are used. When calculating the similarity between ELSA 2000 and its parent node S3 Virge Card, the following values can result:
- Optimistic: When using the optimistic strategy, the similarity \(1.0\) is taken.
- Pessimistic: When using the pessimistic strategy, the weight of the upper node is taken. This is the weight of S3 Virge Card, which is \(\frac{2}{3} \approx 0.6667\) .
- Average: The average strategy calculates the average between the weights. In this case, it is the average of \(\frac{2}{3}\) and \(1.0\) , which is \(\frac{5}{6} \approx 0.8333\) .
Another example is the calculation of the similarity between S3 Graphics Card and its parent node Graphics Card, which is also the root node. There can be the following results:
- Optimistic: The similarity \(1.0\) is taken.
- Pessimistic: The weight of the upper node, Graphics Card, is taken, which is \(0.0\) .
- Average: The average of both weights is taken, which is \(\frac{1}{6} \approx 0.1667\) .
The following parameters can be set for this similarity measure.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| innerNodeInCaseStrategy | Strategy (String) | optimistic | The parameter is used to set the strategy for the similarity computation. It is applied, if an inner node of the taxonomy is used in the case. Three different types exists: optimistic, pessimistic and average. |
| innerNodeInQueryStrategy | Strategy (String) | optimistic | The parameter is used to set the strategy for the similarity computation. It is applied, if an inner node of the taxonomy is used in the query. Three different types exists: optimistic, pessimistic and average. |
To create this measure in the file sim.xml, the class of the atomic object is necessary. For example
<TaxonomyClassic name="SMTaxonomyClassic" class="GraphicsCard"/>
GraphicsCard and it’s defined.At runtime, the measure can be defined as follows:
SMTaxonomyClassic smTaxonomyClassic = (SMTaxonomyClassic) simVal.getSimilarityModel().createSimilarityMeasure(
SMTaxonomyClassic.NAME,
ModelFactory.getDefaultModel().getClass("GraphicsCard")
);
simVal.getSimilarityModel().addSimilarityMeasure(smTaxonomyClassic, "SMTaxonomyClassic");
Classic User Weights #
This measure is very similar to the Classic taxonomy except, that the weights must be set manually. A fundamental prerequisite of this taxonomic similarity measure is that the pre-initialized weights have to be ascending from the root to the deepest leaf (on the lowest level).
For this measure, the same additional strategies as for the classic measure can be used: optimistic, pessimistic and average.
Below is an example of a weighted taxonomy. It was also used to create the test classes.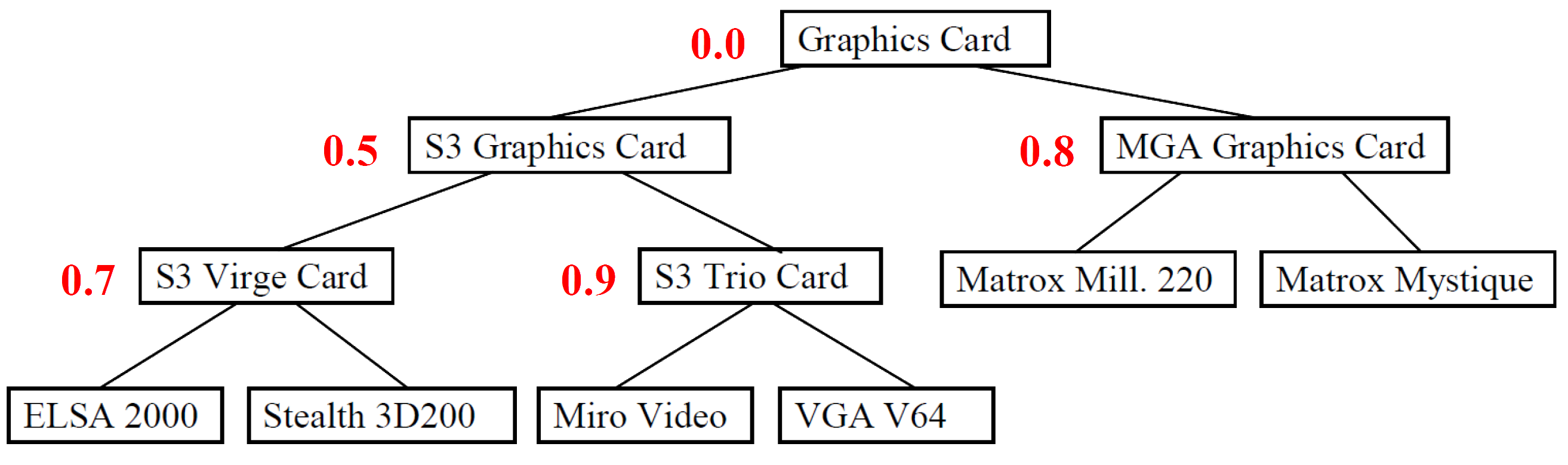
To calculate the similarity between two leaf nodes, the weight of the parent node is always taken. So, the similarity between ELSA 2000 and Miro Video is 0.5, because S3 Graphics Card is the common parent and has this assigned weight. The similarity between ELSA 2000 and Matrix Mill. 220 is 0.0, because their common parent node is the root node, which has a weight of 0.0.
When calculating the similarity between an inner node and one of its ancestors, the different strategies are used. When calculating the similarity between ELSA 2000 and its parent node S3 Virge Card, the following values can result:
- Optimistic: When using the optimistic strategy, the similarity \(1.0\) is taken.
- Pessimistic: When using the pessimistic strategy, the weight of the upper node is taken. This is the weight of S3 Virge Card, which is \(0.7\) .
- Average: The average strategy calculates the average between the weights. In this case, it is the average of \(0.7\) and \(1.0\) , which is \(0.85\) .
Another example is the calculation of the similarity between S3 Graphics Card and its parent node Graphics Card, which is also the root node. There can be the following results:
- Optimistic: The similarity \(1.0\) is taken.
- Pessimistic: The weight of the upper node, Graphics Card, is taken, which is \(0.0\) .
- Average: The average of both weights is taken, which is \(0.25\) .
To create this measure in the file sim.xml, the class of the atomic object is needed as well as the values for the strategies. For each case, whether the case or the query is an inner node, must be determined, which of the three strategies has to be used. As usual, also an individual name is necessary and the default value can be set.
Further, weights for each node must be set. For the identification of the nodes, the value of the node has to be specified. It has to be the exact same value as in the file model.xml, otherwise it would cause an exception. The constraint, that the similarity value the children have must be larger than value of the parents, isn’t checked automatically. A user has to check this, otherwise false similarities would be calculated.
The following parameters can be set for this similarity measure.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| innerNodeInCaseStrategy | Strategy (String) | optimistic | The parameter is used to set the strategy for the similarity computation. It is applied, if a inner node of the taxonomy is used in the case. Three different types exists: optimistic, pessimistic and average. |
| innerNodeInQueryStrategy | Strategy (String) | optimistic | The parameter is used to set the strategy for the similarity computation. It is applied, if a inner node of the taxonomy is used in the query. Three different types exists: optimistic, pessimistic and average. |
For example
<TaxonomyClassicUserWeights name="SMTaxonomyClassicUserWeights" class="GraphicsCard" innerNodeInCaseStrategy="optimistic" innerNodeInQueryStrategy="average">
<Node value="Graphics Card" weight="0.0"/>
<Node value="S3 Graphics Card" weight="0.5"/>
<Node value="MGA Graphics Card" weight="0.8"/>
<Node value="S3 Virge Card" weight="0.7"/>
<Node value="S3 Trio Card" weight="0.9"/>
</TaxonomyClassicUserWeights>
would create a Classic User Weight taxonomy measure, which uses the atomic class GraphicsCard and it’s taxonomy order. For both cases it uses the optimistic strategy.
At runtime, the measure can be defined as follows:
SMTaxonomyClassicUserWeights smTaxonomyClassicUserWeights = (SMTaxonomyClassicUserWeights) simVal.getSimilarityModel().createSimilarityMeasure(
SMTaxonomyClassicUserWeights.NAME,
ModelFactory.getDefaultModel().getClass("GraphicsCard")
);
smTaxonomyClassicUserWeights.setInnerNodeInCaseStrategy(Strategy.OPTIMISTIC);
smTaxonomyClassicUserWeights.setInnerNodeInQueryStrategy(Strategy.AVERAGE);
smTaxonomyClassicUserWeights.setWeight(graphicsCard, 0.0);
smTaxonomyClassicUserWeights.setWeight(s3GraphicsCard, 0.5);
smTaxonomyClassicUserWeights.setWeight(mgaGraphicsCard, 0.8);
smTaxonomyClassicUserWeights.setWeight(s3VirgeCard, 0.7);
smTaxonomyClassicUserWeights.setWeight(s3TrioCard, 0.9);
simVal.getSimilarityModel().addSimilarityMeasure(
smTaxonomyClassicUserWeights, "SMTaxonomyClassicUserWeights"
);
Here, graphicsCard, s3GraphicsCard, mgaGraphicsCard, s3VirgeCard and s3TrioCard need to be atomic objects of the class GraphicsCard. Otherwise, this would cause an exception.
Node Height #
This measure computes the similarity between two nodes based on the height of the nodes. To calculate the similarity between two nodes the common parent of the nodes is searched and the heights of the nodes, which start with 1 for the root and increases the height for each level, are sourced.
Similar to the measure for the Classic User Weighted taxonomy, there are three different strategies for the calculation of the similarity:
- Optimistic: \(sim(q,c) = \frac{height(commonParent(q,c))}{minimum(height(q),height(c))}\)
When using the optimistic strategy, the minimum level of the compared nodes is taken for the calculation.
- Average: \(sim(q,c) = \frac{height(commonParent(q,c))}{\frac{height(q)+height(c)}{2}}\)
When using the average strategy, the average of the levels of the compared nodes is taken for the calculation.
- Pessimistic: \(sim(q,c) = \frac{height(commonParent(q,c))}{maximum(height(q),height(c))}\)
When using the pessimistic strategy, the maximum level of the compared nodes is taken for the calculation.
Below is an example of a taxonomy. It was also used to create the test classes.
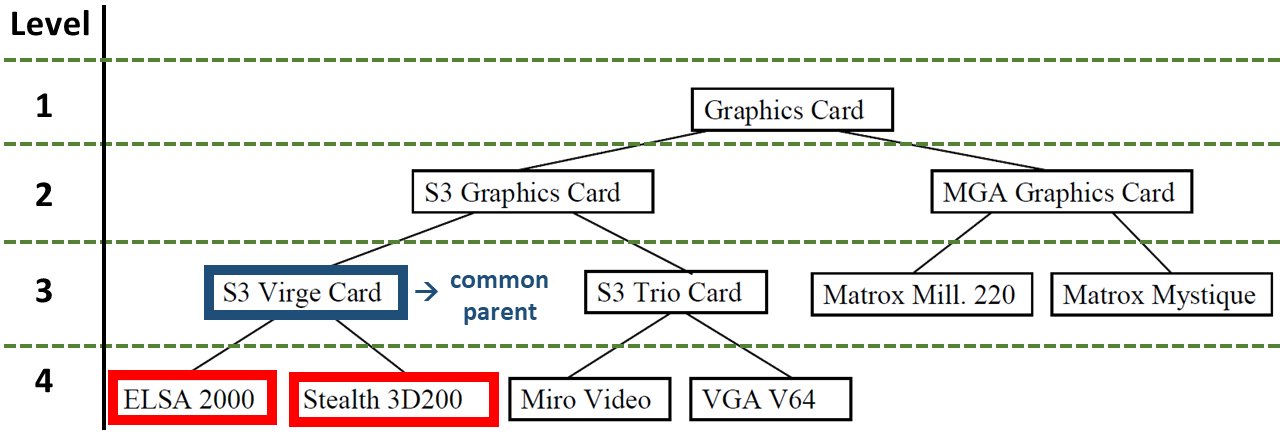
To calculate the similarity between the nodes ELSA 2000 and Stealth 3D200 their height and the height of their common ancestor node are needed. These two nodes are located at level 4, their common parent node, S3 Virge Card, at level 3. Because the levels of the two considered nodes are equal, the strategies will return the same result. The minimum and maximum level are equal and so the average is equal, too. The similarity is \(\frac{3}{4}\) .
Below is a second example of a taxonomy. It’s the same taxonomy as before, but with different nodes in query and case.
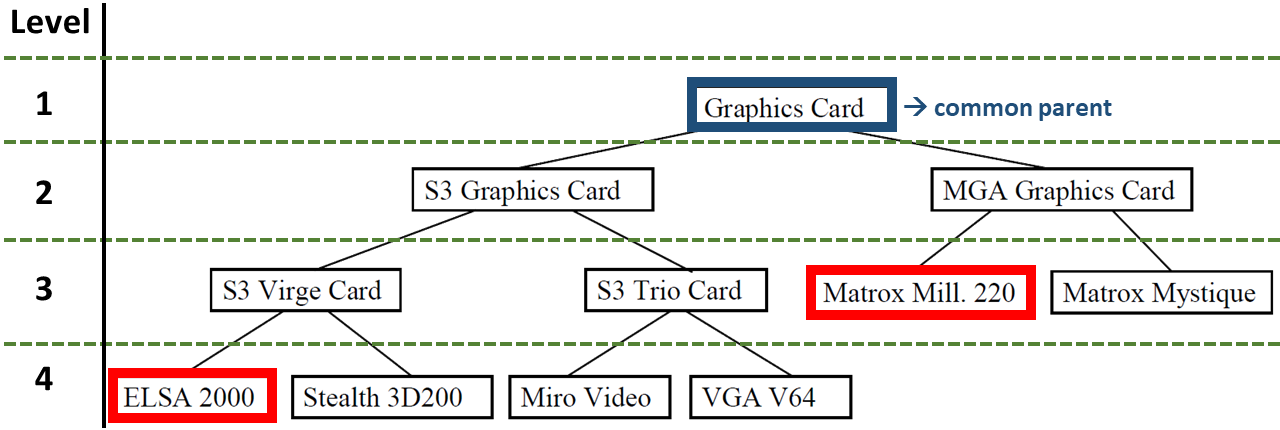
When calculating the similarity between nodes at different levels, the strategies return different results. The node ELSA 2000 is at level 4, the node Matrox Mill. 220 at level 3. Their common ancestor is the root node Graphics Card at level 1. The following results can be computed:
- Optimistic: \(\frac{1}{3}\) .
- Pessimistic: \(\frac{1}{4}\) .
- Average: \(\frac{1}{3.5} = \frac{2}{7} \) .
The following parameters can be set for this similarity measure.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| strategy | Strategy (String) | pessimistic | The parameter is used to set the strategy for the similarity computation. Three different types exists: optimistic, pessimistic and average. |
To create this measure in the file sim.xml, the class of the atomic object and the selected strategy are needed. As usual, also an individual name is necessary and the default value can be set. For example
<TaxonomyNodeHeight name="SMTaxonomyNodeHeight" class="GraphicsCard" strategy="optimistic"/>
would create a Node Height taxonomy measure, which uses the atomic class GraphicsCard and it’s order. It uses the optimistic strategy.
At runtime, the measure can be defined as follows:
SMTaxonomyNodeHeight smTaxonomyNodeHeight = (SMTaxonomyNodeHeight) simVal.getSimilarityModel().createSimilarityMeasure(
SMTaxonomyNodeHeight.NAME,
ModelFactory.getDefaultModel().getClass("GraphicsCard")
);
smTaxonomyNodeHeight.setStrategy(Strategy.OPTIMISTIC);
simVal.getSimilarityModel().addSimilarityMeasure(
smTaxonomyNodeHeight, "SMTaxonomyNodeHeight"
);
Path #
This measure computes the similarity based on the shortest path between an element in the query and an element in the case based on the taxonomy. Thereby, each step upward in the taxonomy and each step downward is counted and each of them multiplied with an additional weight. The weights can be chosen freely. However, they will be normalized by the system.
In order to calculate the similarity between two nodes in the taxonomy, first, the longest path in the taxonomy is determined. The longest path is required to normalize the calculated similarity value later. Therefore, the weights for up and down are already used:
\( maxPathWeighted= weightUp * \#maxStepsUpward + weightDown * \#maxStepsDownward \)Thus, the steps upward of the deepest node to the root node as well as the steps downward to the deepest node are determined, i.e., the height of the deepest node is taken and doubled. It is important that the value of maxPathWeighted is always the longest possible path length. It is important to note that using freely chosen weights for up and down can lead to two paths of the same length being considered differently. All in all, every time an overestimating path length is used.
For similarity calculation, the common parent node of the query node and the case node is determined. The path is traversed up from the query node to the common parent node and down to the case node. The path length is calculated as follows:
\(nodePathWeighted = weightUp * \#stepsUpward + weightDown * \#stepsDownward\)Using the values for nodePathWeighted and maxPathWeighted, the final similarity is calculated as follows:
\(sim = \frac{maxPathWeighted - nodePathWeighted }{maxPathWeighted}\)Given is the following example of a taxonomy.
To calculate the similarity between the nodes ELSA 2000 and Matrox Mill. 220, the steps to reach one node from the other are counted. These are 3 steps up and 2 steps down in the taxonomy. The similarity depends on the chosen weights for up and down:
If both weights are 1, they will be normalized using the formula \( normalizedWeight = \frac{oldWeight}{weightSum}\) to 0.5. The value for maxPathWeighted is \( maxPathWeighted= 0.5 * 3 + 0.5 * 3 = 3\) . The value for nodePathWeighted is \( nodePathWeighted = 0.5 * 3 + 0.5 * 2 = 2.5\) . All in all, the similarity is \(sim = \frac{3 - 2.5}{3} = \frac{0.5}{6} = 0.0833\) .
If the weight for up is 0.2 and the weight for down is 0.3, both weights will be normalized to 0.4 for up and 0.6 for down. Using these weights, the value for maxPathWeighted is \( maxPathWeighted= 0.4* 3 + 0.6 * 3 = 3\) . The value for nodePathWeighted is \( nodePathWeighted = 0.4* 3 + 0.6 * 2 = 2.4\) . Finally, the similarity is \(sim = \frac{3 - 2.4}{3} = \frac{0.6}{3} = 0.2\) .
The following parameters can be set for this similarity measure.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| up | Weight (int) | 1 | The parameter is used to set the weight for steps upwards in the path between two nodes. |
| down | Weight (int) | 1 | The parameter is used to set the weight for steps downwards in the path between two nodes. |
To create this measure in the similarity model sim.xml, the class of the atomic object is needed as well as weights for up and down. Furthermore, an individual name is necessary and the default value can be set. For example
<TaxonomyPath name="SMTaxonomyPath" class="GraphicsCard" up="1" down="1"/>
would create a Path taxonomy measure, which uses the atomic class GraphicsCard and it’s order. The weights for up and down are both 1. Thus, the similarity for this measure will always be 1.0.
At runtime, the measure can be defined as follows:
SMTaxonomyPath smTaxonomyPath = (SMTaxonomyPath) simVal.getSimilarityModel().createSimilarityMeasure(
SMTaxonomyPath.NAME,
ModelFactory.getDefaultModel().getClass("GraphicsCard")
);
smTaxonomyPath.setWeightUp(1.0);
smTaxonomyPath.setWeightDown(1.0);
simVal.getSimilarityModel().addSimilarityMeasure(smTaxonomyPath, "SMTaxonomyPath");
Comparison of String measures #
In the following, a table of different strings as queries and cases with their corresponding similarities is shown. The code, which was used to compute the similarities, is located in the class StringSimilarityMeasureComparison.
For this comparison, the following similarity measures are configured as follows:
- Measures String Equal, Levenshtein and cosine are case-insensitive.
- Measures cosine and Term Count use
[^\\w]as delimiter.
The following similarity values are obtained:
| Query | Case | Levenshtein | Cosine | JaroWinkler | TermCount | Equal | N-Gram | Wildcard |
|---|---|---|---|---|---|---|---|---|
| "" | "" | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | -1.0 | 1.0 |
| "" | “ ” | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | -1.0 | 0.0 |
| “aaapppp” | "" | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | -1.0 | 0.0 |
| "" | “aaapppp” | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | -1.0 | 1.0 |
| “foo” | “foo” | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 0.0 |
| “foo” | “FoO” | 1.0 | 1.0 | 0.55555555 | 1.0 | 1.0 | 0.0 | 0.0 |
| “foo” | “foo " | 0.75 | 1.0 | 0.94166666 | 1.0 | 0.0 | 0.5 | 0.0 |
| “foo” | “foo ” | 0.6 | 1.0 | 0.90666666 | 1.0 | 0.0 | 0.33333333 | 0.0 |
| “foo” | “ foo” | 0.6 | 1.0 | 0.51111111 | 1.0 | 0.0 | 0.33333333 | 0.0 |
| “ foo” | “ foo” | 0.71428571 | 0.0 | 0.92380952 | 1.0 | 0.0 | 0.6 | 0.0 |
| “frog” | “fog” | 0.75 | 0.0 | 0.92499999 | 1.0 | 0.0 | 0.0 | 0.0 |
| “fly” | “ant” | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| “elephant” | “hippo” | 0.125 | 0.0 | 0.44166666 | 1.0 | 0.0 | 0.0 | 0.0 |
| “hippo” | “elephant” | 0.125 | 0.0 | 0.44166666 | 1.0 | 0.0 | 0.0 | 0.0 |
| “ABC Corporation” | “ABC Corp” | 0.53333333 | 0.49999999 | 0.90666666 | 1.0 | 0.0 | 0.46153846 | 0.0 |
| “ProCAKE” | “ProCAKE Framework” | 0.41176470 | 0.70710678 | 0.88235294 | 0.5 | 0.0 | 0.33333333 | 0.0 |
| “ProCAKE” | “ProCAKE - The Process-oriented Case-based Knowledge Engine” | 0.12068965 | 0.35355339 | 0.82413793 | 0.125 | 0.0 | 0.10714285 | 0.0 |
| “C://Users/Public/data42.xml” | “D://Data/data42.xml” | 0.51851851 | 0.44721359 | 0.65654877 | 0.8 | 0.0 | 0.44 | 0.0 |
Some remarks on the results:
The Wildcard measure performs an exact matching as long as no no specific Wildcard symbols are used.
The Levenshtein measure produces high similarity values when comparing small strings such as “frog” and “fog”. If one of both strings is significantly longer than the other, the similarity values will become very small even if one string is contained in the other.
The Jaro Winkler produces higher similarity values than the Levenshtein if both strings have the same prefix such as in the example of “frog” and “fog” where the similarity is \(0.9249\) .
The N-Gram returns an invalid similarity value for the first four cases, because n is higher than the length of the strings.