This page explains, how the fuzzy similarity is computed. The complete derivation of the formula is listed.

Numeric Fuzzy similarity #

The fuzzy similarity needs two numeric values query q and case c. These numbers represent the x-values of a point in a coordinate system. The y-value of these two points is per default 1. So, the points are Q(q|1) and C(c|1). If the x-value is 0, the similarity is also 0.0. In a special case, when both values are 0, the similarity is 1.0.

Important note: The complete formula just works, when the case is higher than the query or equal to it. Otherwise, the values need to be swapped. This is considered in the implementation.

Also, a value for spread is needed. This value specifies the length of a line the x-axis, which depends on the x-value of the point. The value isn’t allowed to be 0 or negative. The spread is the same value for q and c. But the length of the line hasn’t to be.

Using the points Q and C and the spread-value, a triangle is formed. The spread-value is used as the longest side of this triangle.

This is illustrated in the following graph:

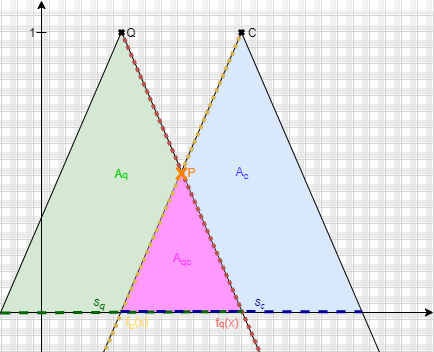
The spread-values \(s_{q}\) and \( s_{c}\) are not necessarily the same ones. They are computed as follows:

The fuzzy similarity needs the size of the areas. \(A_{q}\) , \(A_{c}\) and \(A_{qc}\) need to be computed.

The two areas \(A_{q}\) and \(A_{c}\) can be computed by using the default formula for the area of a triangle \(A = \frac{ 1 }{ 2 } * height + longestLine\) .

The height is always 1. So, the size is computed as follows:

The computation of \(A_{qc}\) is more complex. The the longest line can be computed using the formula \(2 * (q + s - p_{x})\) . When using the x-value of Q and adding half of \( s_{c}\) , the second point of the triangle with the y-value 0 is reached. This point marks also the second point of the triangle \(A_{qc}\) . When subtracting the x-value of P, the half of the line on the x-axis is computed.

So, the formula for the area of \(A_{qc}\) is: \(A_{qc} =\frac{ 1 }{ 2 } * P_{y} * 2 * (q + s_{q} - P_{x}) = P_{y} * (q + s_{q} - P_{x})\)

For this, the coordinates of the point \(P (p_{x}|p_{y})\) are required.

These values can be computed, when making functions out of the crossing lines of the triangles and searching for the crossing point. So, the formulas for the lines \( f_{ q } (x)\) and \( f_{ c } (x)\) are required.

These formulas can be derived by using the default formula \( f(x) = m * x + b\) . For both functions, the values for m and b need to be computed.

The value for m can be computed by the default formula \(m = \frac{ y_{ 2 } - y_{ 1 } }{ x_{ 2 } - x_{ 1 } }\) . Therefore, two points are required, that are on each function.

At first, the formula for \( f_{ q } (x)\) is computed. The point Q is already know. Another point \( Q_{ 0 }\) can be computed. The y-value for this point is 0, so it’s the second point, where the triangle meets the x-axis. So, it’s x-value is \( q + \frac{1}{2} * s_{q}\) . So, the point is \( Q_{ 0 }(q + \frac{1}{2} * s_{q}|0)\) .

Using the points Q and \( Q_{ 0 }\) , m can be computed: \(m = \frac{ 0 - 1 }{ (q + \frac{1}{2} * s_{q}) - q } = -\frac{ 1 }{ \frac{1}{2} * s_{q} } = -\frac{ 2 }{ s_{q}}\)

So, the formula is \( f_{ q } (x) = -\frac{ 2 }{ s_{q} } * x + b\) . Using the values of one of the points, the value for b can be computed. Here, the point Q is used.

The complete formula is: \( f_{ q } (x) = -\frac{ 2 }{ s_{q} } * x + \frac{ 2 }{ spread } + 1\)

This proceed is repeated for the formula of \( f_{ c } (x)\) . There, the point C is already known. Another point \( C_{ 0 }\) can be computed. The y-value for this point is 0, so it’s the first point, where the triangle meets the x-axis. So, it’s x-value is \( c * \frac{1}{2} * s_{c}\) . So, the point is \( C_{ 0 }(c - \frac{1}{2} * s_{c}|0)\) .

Using the points C and \( C_{ 0 }\) , m can be computed: \(m = \frac{ 0 - 1 }{ (c - \frac{1}{2} * s_{c}) - c } = -\frac{ 1 }{ -\frac{1}{2} * s_{c} } = \frac{ 2 }{ s_{c}}\)

So, the formula is \( f_{ c } (x) = \frac{ 2 }{ s_{c} } * x + b\) . Using the values of one of the points, the value for b can be computed. Here, the point Q is used.

The complete formula is: \( f_{ c } (x) = \frac{ 2 }{ s_{c} } * x -\frac{ 2 }{ spread } + 1\)

Using both formulas, the crossing point of the lines can be computed by \( f_{ q } (x) = f_{ c } (x)\) .

Using the value in one of the functions, the y-value can be computed.

So, the coordinates for P are computed: \( P (\frac{2 * q * c}{ q + c} | -\frac{ 4 * c }{ spread * ( c + q) } +\frac{ 2 }{ spread } + 1 )\)

In the implementation, the coordinates are just shown as \( P (\frac{2 * q * c}{ q + c} | -\frac{ 2 }{ q * spread } + p_{x} + \frac{2}{spread} + 1)\) .

Note: If the y-value of P is negative, there is no crossing area. So in this case, the similarity will be \( 0.0\) and the computation stopped.

Using this formulas, the formula for the computation of \(A_{qc}\) is:

Using the values of the areas \(A_{q}\) , \(A_{c}\) and \(A_{qc}\) , the maximum of \(\frac{A_{qc}}{A_{q}}\) and \(\frac{A_{qc}}{A_{c}}\) is computed. This is the value for the similarity.