Numeric #
This page contains the following content:
The following measures are implemented for numeric types (Integer, Double) according to the definitions by Ralph Bergmann1. Except for the Fuzzy measure, these measures are distance-based and therefore, these distance-based measures can also be applied to the chronological types (Time, Timestamp, Date).
The use of the numeric measures for chronological types is analog to the use of the numeric types. However, it is not possible to compare chronological objects of different types with each other.
Restricting value ranges #
It is possible to restrict the possible value ranges for numeric and chronological types. All here listed similarity measures can work with the restriction. For further information, have a look at Restricting Value Ranges.
Distance value #
For all measures except the Fuzzy measure, the similarity between two numbers (here: query value
\(q\)
and case value \(c\)
) is usually calculated by using the so called
distance between those two numbers. In the formulas the letter \(d\)
stands for distance. The
smaller \(d\)
is, the more similar are the two values. \(d=0\)
will lead to the
similarity value \(sim=1\)
.
The formula for the calculation of \(d\)
is \(d(q,c) = |q-c|\)
. Some measures use
normalized version (Exponential and Sigmoid)
\(d_{norm}(q,c) = \frac{d(q,c)}{max-min}\)
. It does not matter whether the objects are of numeric
or chronological type. The values of \(min\)
and \(max\)
depend on whether
\(q\)
and \(c\)
are of type Integer, Double or Chronological:
case 1 (
queryandcaseare of typeInteger): \(max-min = Integer.MAX\_VALUE - Integer.MIN\_VALUE\) .case 2 (
queryandcaseare of typeDouble): In this case \(min = Double.MIN\_VALUE\) and \(max = Double.MAX\_VALUE\) . However, since \(max - min\) is larger than \(Double.MAX\_VALUE\) , the value could not be represented by theDoubletype inJava. Therefore, the result is defined as \(max-min = Double.MAX\_VALUE\) .case 3 (
queryandcaseare of theChronologicaltype): In this case the minimum and maximum points in time based on \(min = Long.MIN\_VALUE\) and \(max = Long.MAX\_VALUE\) are used that can be mapped in Java are used. For all three inherited classesDate,TimeandTimestampare \(min\) and \(max\) the same.
Strategies for numeric measures #
In ProCAKE there are three asymmetric strategies for the numeric measures, which influence the similarity value:
- CaseHigherThanQuery: If the case value is higher than the query value, the similarity will always be \(0.0\) .
- QueryHigherThanCase: If the query value is higher than the case value, the similarity will always be \(0.0\) .
- None: This is the default strategy. When using this one, no asymmetric zero out will happen.
The following parameters exist for all numeric similarity measures.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| strategy | Strategy (String) | none | The parameter is used to set the strategy for the similarity computation. Three different types exists: CaseHigherThanQuery, QueryHigherThanCase and none. |
The values can be set in the XML file. For example:
<NumericMeasure name="NumericMeasure" class="Double" alpha="6" asymmetricZeroOutStrategy="query_higher_than_case"/>
Otherwise, the strategy can be set during runtime by using the method setAsymmetricStrategy(ZERO_OUT_STRATEGIES strategy). This can look like:
smNumericMeasure.setAsymmetricStrategy(ZERO_OUT_STRATEGIES.CASEHIGHERTHANQUERY);
Linear #
In most cases the similarity between two numeric values can be described by a linear function. The idea is that the similarity decreases linearly in an interval \([min,max]\) with the increase of difference between the two values.
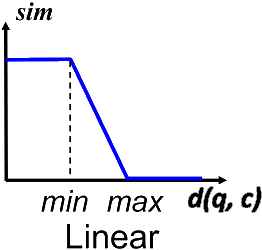
If the distance is smaller than the minimum, the value for the similarity is \(1.0\) . If the distance is higher than the maximum, the value for the similarity is \(0.0\) . For the values between, the similarity is calculated by the formula \(\frac{max-d(q,c)}{max-min}\) .
Formalized, the similarity calculation works as follows:
\(sim(q,c) = \begin{cases} 1 &\text{, if } d(q,c) \lt min \\ \frac{max-d(q,c)}{max-min} &\text{, if } min \leq d(q,c) \leq max \\ 0 &\text{, if } d(q,c) \gt max \end{cases}\)The following graph shows the similarity depending on the calculated distance.
The following parameters can be set for this similarity measure.
Numeric parameters:
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| min | Bound (int) | 0.0 | The parameter is used to set the minimum bound of the interval. |
| max | Bound (int) | Double.MAX_VALUE/Integer.MAX_VALUE/Highest upper bound (interval range) | The parameter is used to set the maximum bound of the interval. If it wasn’t set, a warning is issued by the logger when the measure is initialized. |
Chronological parameters:
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| min | Bound (int) | DateObject.MIN_VALUE/TimeObject.MIN_VALUE/TimestampObject.MIN_VALUE | The parameter is used to set the minimum bound of the interval. |
| max | Bound (int) | DateObject.MAX_VALUE/TimeObject.MAX_VALUE/TimestampObject.MAX_VALUE /Highest upper bound (interval range) | The parameter is used to set the maximum bound of the interval. If it wasn’t set, a warning is issued by the logger when the measure is initialized. |
The values for \(min\)
and \(max\)
can be set, when creating the measure. Either in the sim.xml:
<NumericLinear name="SMNumericLinear" class="Double" min="0" max="10"/>
Or during runtime:
SMNumericLinear smNumericLinear = (SMNumericLinear) simVal.getSimilarityModel().createSimilarityMeasure(
SMNumericLinear.NAME,
ModelFactory.getDefaultModel().getDoubleSystemClass()
);
try {
smNumericLinear.setMaximum(10);
smNumericLinear.setMinimum(0);
} catch (InvalidAttributeValueException exception) {
exception.printStackTrace();
}
simVal.getSimilarityModel().addSimilarityMeasure(smNumericLinear, "SMNumericLinear");
Here it must be noted that the methods setMinimum and setMaximum can each throw an InvalidAttributeValueException. Therefore, these must be handled with a try-catch clause.
If no value is set for \(min\) , it is set to the default value of \(0.0\) . Furthermore, it is not possible to set \(min\) to a value below \(0.0\) .
If no value is set for \(max\) , the maximum value for the data class of case and query is chosen. So, if they are double objects, the maximum Double value is set as maximum. If they are integer objects, the maximum Integer value is set as maximum.
It is also possible, to use this measure with numeric objects, that contain an interval range. If no value for \(max\) is set, the highest possible distance is used. This is calculated as the distance of the highest upper bound and the smallest lower bound.
Threshold #
Threshold functions should be used, if the contribution of an attribute to the utility is binary in the sense that up to a certain difference the case is useful and beyond it is not useful.
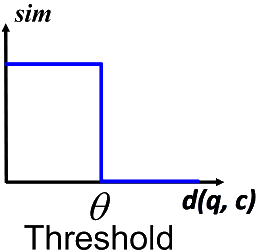
There is also the Threshold value \(\theta\) , which has to be set. The value for the similarity depends on the \(\theta\) value. If the distance \(d(q,c)\) is smaller than \(\theta\) , the similarity is \(1.0\) . Otherwise, the similarity is \(0.0\) .
The formula for the similarity calculation is as follows:
\(sim(q,c) = \begin{cases} 1 &\text{, if } d(q,c) \lt \theta \\ 0 &\text{, if } d(q,c) \geq \theta \end{cases}\)The following figure illustrates the similarity function:
The following parameters can be set for this similarity measure.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| threshold | threshold (double) | 1.0 | The parameter expects a Double value given, that defines a threshold value \(\theta\) . If the distance \(d(q,c)\) is smaller than \(\theta\) , the similarity is \(1.0\) . Otherwise, the similarity is \(0.0\) . |
The similarity measure can be defined in the sim.xml like below:
<NumericThreshold name="SMNumericThreshold" class="Double" threshold="1"/>
To create this measure during runtime, use the following code:
SMNumericThreshold smNumericThreshold = (SMNumericThreshold) simVal.getSimilarityModel().createSimilarityMeasure(
SMNumericThreshold.NAME,
ModelFactory.getDefaultModel().getDoubleSystemClass()
);
smNumericThreshold.setThreshold(1.0);
simVal.getSimilarityModel().addSimilarityMeasure(smNumericThreshold, "SMNumericThreshold");
Fuzzy #
Note that Fuzzy is not applicable for chronological types, because it is not a distance-based measure, so it can only be used for numerics.
This measure is providing fuzzy similarity functionality, according to the paper by Ahmed et al.2 (see p.13 for a visual description). A spread is defined, which allows triangle-areas on those values. If the areas of the compared values overlap, this indicates a similarity. \(max(Overlap/area1, Overlap/area2)\) is then the similarity.
A complete description, how the fuzzy similarity is computed in detail, can be found here.
The following parameters can be set for this similarity measure.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| spread | Length (double) | 1.0 | The parameter expects a Double value given, that specifies the length of a line the x-axis, which depends on the x-value of the point. A detailed explanation can be found here. |
The similarity measure can be defined in the sim.xml like below:
<NumericFuzzy name="SMNumericFuzzy" class="Double" spread="0.5"/>
To create this measure during runtime, use the following code:
SMNumericFuzzy smNumericFuzzy = (SMNumericFuzzy) simVal.getSimilarityModel().createSimilarityMeasure(
SMNumericFuzzy.NAME,
ModelFactory.getDefaultModel().getDoubleSystemClass()
);
smNumericFuzzy.setSpread(0.5);
simVal.getSimilarityModel().addSimilarityMeasure(smNumericFuzzy, "SMNumericFuzzy");
Exponential #
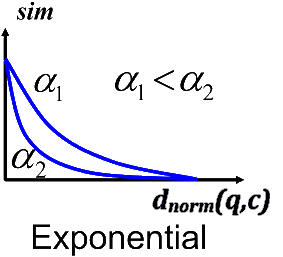
One possibility to describe the similarity between two numeric values is by an exponential function. The semantics of such a similarity function is that little differences between the two values cause a big decrease of similarity. The larger the parameter \(\alpha\) , the faster is the decrease. Make sure that \(\alpha > 1\) .
\(sim(q,c) = e^{d_{norm}(q,c) \cdot (-\alpha)}\)The following graph shows the similarity values for two different values of \(\alpha\) , namely \(\alpha_1\) and \(\alpha_2\) with \(\alpha_1 < \alpha_2\) . As already said, the sim value decreases faster the larger \(\alpha\) is.
The following parameters can be set for this similarity measure.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| alpha | Growth (double) | 1.0 | The parameter expects an Integer value given, that controls the growth of the exponential function for the similarity. The larger alpha is, the faster the function grows. |
The similarity measure can be defined in the sim.xml like below:
<NumericExponential name="SMNumericExponential" class="Double" alpha="6"/>
To create this measure during runtime, use the following code:
SMNumericExponential smNumericExponential = (SMNumericExponential) simVal.getSimilarityModel().createSimilarityMeasure(
SMNumericExponential.NAME,
ModelFactory.getDefaultModel().getDoubleSystemClass()
);
smNumericExponential.setAlpha(6.0);
simVal.getSimilarityModel().addSimilarityMeasure(smNumericExponential, "SMNumericExponential");
Sigmoid #
Sigmoid functions can also be used to compare numeric values. The parameter \(\theta \geq 0\) specifies the distance value at which the similarity is \(0.5\) . The parameter \(\alpha>0\) specifies the steepness of the similarity decrease: the smaller \(\alpha\) the steeper is the decrease.
\(sim(q,c) = \frac{1}{e^{\frac{d_{norm}(q,c)-\theta}{\alpha}}+1}\)The following graph shows the similarity values for two different values of \(\alpha\) , namely \(\alpha_1\) and \(\alpha_2\) with \(\alpha_1 \lt \alpha_2\) . As already said, the sim value decreases more steeply the larger \(\alpha\) is.

The following parameters can be set for this similarity measure.
| Parameter | Type/Range | Default Value | Description |
|---|---|---|---|
| alpha | Growth (double) | 1.0 | The parameter expects a Double value given, that specifies the steepness of the similarity decrease. The smaller alpha, the steeper is the decrease. |
| theta | Growth (double) | 1.0 | The parameter is used to set the distance value, at which the similarity is 0.5. |
The similarity measure can be defined in the sim.xml like below:
<NumericSigmoid name="SMNumericSigmoid" class="Double" alpha="0.1" theta="0.5"/>
To create this measure during runtime, use the following code:
SMNumericSigmoid smNumericSigmoid = (SMNumericSigmoid) simVal.getSimilarityModel().createSimilarityMeasure(
SMNumericSigmoid.NAME,
ModelFactory.getDefaultModel().getDoubleSystemClass()
);
smNumericSigmoid.setAlpha(0.1);
smNumericSigmoid.setTheta(0.5);
simVal.getSimilarityModel().addSimilarityMeasure(smNumericSigmoid, "SMNumericSigmoid");
Ralph Bergmann: Experience Management: Foundations, Development Methodology, and Internet-Based Applications. Lecture Notes in Computer Science 2432, Springer 2002, ISBN 3-540-44191-3 ↩︎
Mobyen Uddin Ahmed, Shahina Begum, Peter Funk, Ning Xiong, Bo von Schéele: Case-based Reasoning for Diagnosis of Stress using Enhanced Cosine and Fuzzy Similarity. Tran. CBR 1(1): 3-19 (2008) ↩︎